2025年09月09日
みなさん、こんにちは！
幾何公差シリーズの第二弾となります。今回解説するのは以下の公差です。
-
- 位置度
- 同心度
- 同軸度
- 対称度
- 線の輪郭度
- 面の輪郭度
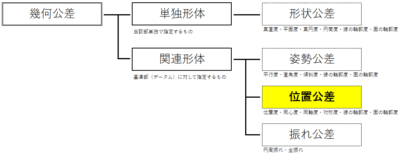
1. データムとは？ 『単独形体』と『関連形体』
本題に入る前に、幾何公差を理解する上で、必須になる要素を解説します。
幾何公差は大きく分けて『単独形体』と『関連形体』があります。“真っすぐさ”や“まん丸さ”など、単独の要素で成立する単独形体に対し、関連形体は“直角度”や“平行度”など、基準になる箇所との関連性で指定する必要があります。
■単独形体・・単独で指定する（対象）「形状公差」
■関連形体・・基準に対して指定する（対象）「姿勢公差」「位置公差」「振れ公差」
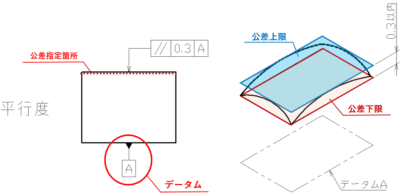
基準になる箇所を「データム」と言い、記号は四角で囲んだアルファベットが用いられます。基準面(線)に接する形で三角形を明示し、頂点とアルファベットと線で結んで明記します。
公差指定箇所については、公差記号・公差・データム記号をセットで明記します。
下図の例では、赤の破線部に平行度が指定されています。この場合、赤丸のデータムAで指示されている線を基準に、指定箇所は0.3の範囲に収まっていなければなりません。
お待たせしました。データムの理解が深まったところで、本題に入ります！
2. 位置公差 ~位置度・同心度・同軸度・対称度・線の輪郭度・面の輪郭度~
今回は関連形体のひとつ、位置公差に属するものの解説になります。
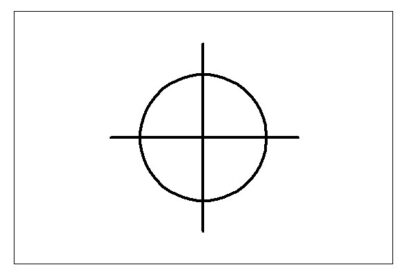
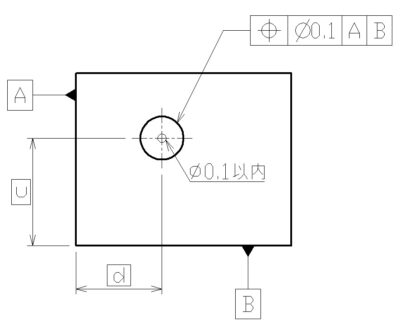
①位置度
データムに対する「位置」を規定するもの。
下図の場合、寸法ｃおよび寸法ｄの距離が、それぞれ0.1の範囲内（φ0.1）に収まっていなければなりません。
公差記号
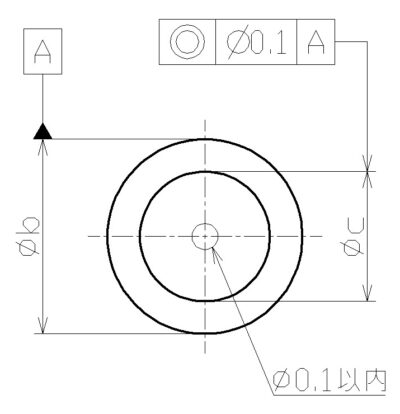
②同心度
データムに対する「芯のズレ」を規定するもの。
下図の場合、φｄの中心点に対するφｃの中心点のズレが、φ0.1以内に収まっていなければなりません。
公差記号
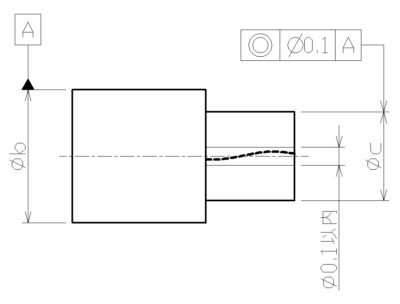
③同軸度
データムに対する「芯のズレ」を規定するもの。
同心度と同じ公差記号で示されますが、こちらは穴を横から見た状態での指示になります。
下図の場合、φｄの軸芯に対するφｃの軸芯ズレが、φ0.1以内に収まっていなければなりません。
公差記号
④対称度
データムに対する「対称さ」を規定するもの。
下図の場合、データムAの中心平面に対し、寸法ｂ部それぞれの面の中心面が±0.05の範囲におさまっていなければなりません。
公差記号
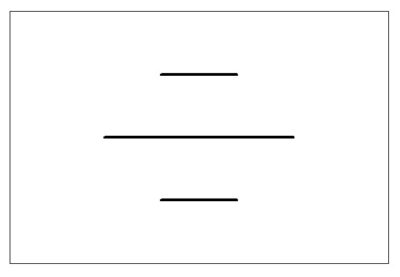
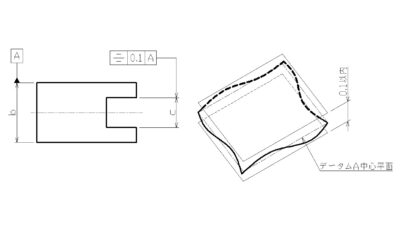
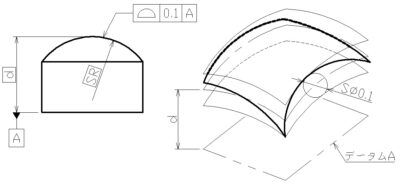
⑤線の輪郭度
指定される線について、「歪み」および「データムに対する位置関係」を規定するもの。
公差記号
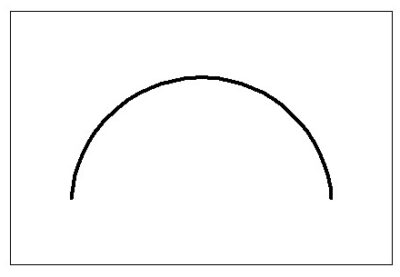
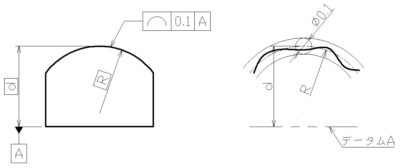
⑥面の輪郭度
指定される面について、「歪み」および「データムに対する位置関係」を規定するもの。
公差記号
という事で、今回はここまで！
④と⑤の輪郭度は、3回目の登場です。
単独で「形状公差」、データム基準で「姿勢公差・位置公差」と大活躍ですね。
幾何公差シリーズは次回で最終回になります。お楽しみに～👋
03-3658-8251